Prefix Notation and Hybrid Version
In the last post I introduces the
prefix notation for “encoding” equations.
I also showed that the number of arguments for each operator needs to be fixed, so
\(a + b + c\) has to turn into + a + b c.
This of course introduces lots of tokens when there are multiplications or additions with many elements.
Thus, I thought it might be a good idea to reintroduce parentheses just for addition and multiplication,
but with a twist: Effectively there is only a closing parenthese.
Example: \(a+b+c\) becomes +( a b c ) or to make clear what the tokens are, here as a list: [ +(, a, b, c, ) ].
Below is the token length distribution for squared amplitudes for QED up to \(3 \to 3\).
The squared amplitudes have all been simplified using sympy’s factor function, since
I found that it gives the shortest token lenghts.
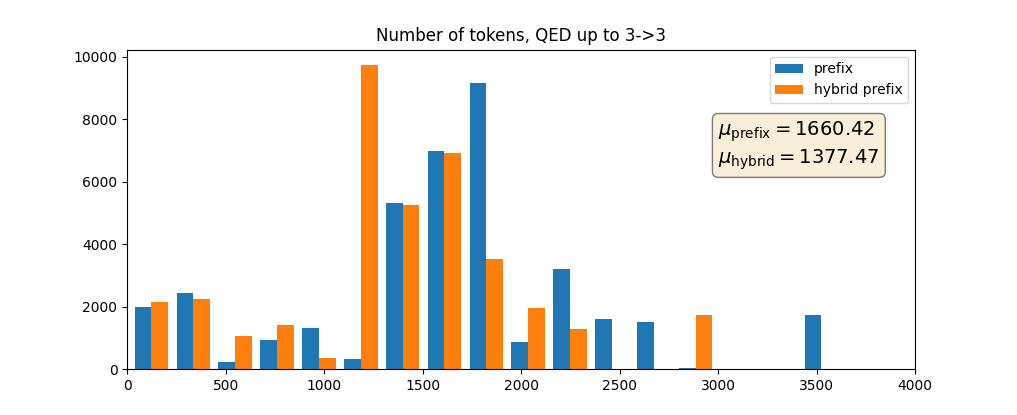
As we can see, the hybrid version lowered the token lengths by quite a bit, but more than 200-500 are not feasable anyway … so I don’t know what to make of this yet.